Gruppenarbeit: Simulation einer 4-stufigen Bernoulli-Kette mit einem Galton-Brett
Der berühmte britische Naturwissenschaftler Charles Darwin (1809-1882) begründete die Evolutionstheorie. Er befasste sich mit Fragen der Vererbung und suchte hierfür nach einfachen Modellen. Sein Cousin Sir Francis Galton (1822-1911) hatte dazu eine Idee. Er entwickelte einen Versuch, der als sogenanntes Galton-Brett in die Wissenschaftsgeschichte einging.
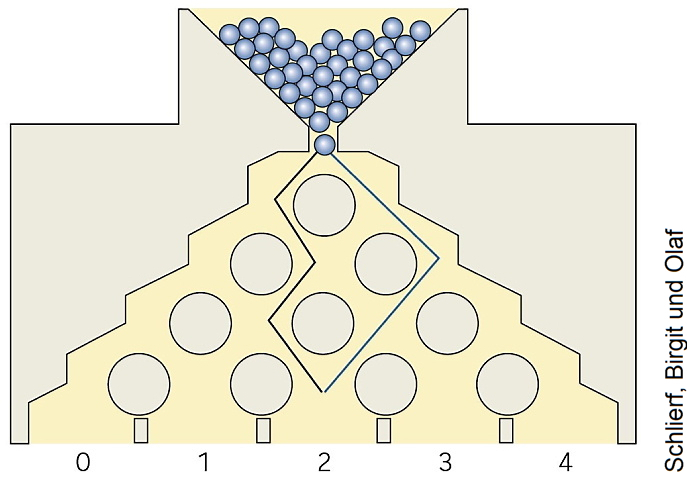
In der Abbildung ist ein sogenanntes Galtonbrett mit vier
Hindernisreihen dargestellt. Aus einem Trichter laufen Kugeln durch
die Hindernisreihen aus Nägeln. An jedem Nagel werden die Kugeln mit
gleicher Wahrscheinlichkei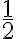t 
entweder nach links (L) oder nach
rechts (R) abgelenkt.
Schließlich fallen Sie in eines der Fächer mit den Nummern 0, 1, 2, 3, oder 4. Die Nummern geben an, wie oft die Kugel auf ihren Weg durch das Nagelbrett nach rechts (aus der Sicht des Betrachters) abgelenkt wurde.
Sie können mithilfe des Applets mehrere Versuche mit einem solchen Brett simulieren.
a) Erläutern Sie, wie man mit diesem Galtonbrett einen vierfachen Münzwurf simulieren kann, bei dem Zahl als Erfolg gewertet wird.
b) Wiederholen Sie die Simulation 100-, 500- und 1000-mal und notieren Sie die Anzahl von Zahl für einen vierfachen Münzwurf.
c) Welche Anzahl von Zahl kam am häufigsten vor? Warum war dieses Ergebnis zu erwarten?
d) Tragen Sie Ihre Ergebnisse zusammen und finden Sie damit eine Häufigkeitsverteilung der Anzahlen für Zahl bei 20 000 Wiederholungen.
e) Berechnen Sie auch die Wahrscheinlichkeiten, dass eine Kugel in das Fach mit der Nummer 0, 1, 3, 4 fällt und vergleichen Sie die Ergebnisse mit der Häufigkeitsverteilung in Teilaufgabe c).
f) Ändern Sie im Applet die Anzahl der Hindernisreihen und bearbeiten Sie damit die Teilaufgaben a) bis e).