Binomialkoeffizient

Die Zahl 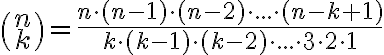 \binom {n} {k} = \frac{n \cdot(n-1) \cdot(n-2) \cdot ... \cdot(n-k+1) }{k \cdot(k-1) \cdot(k-2) \cdot ... \cdot3 \cdot2 \cdot1 } heißt Binomialkoeffizient und wird n über k gelesen. Der Binomialkoeffizient gibt die Anzahl der Möglichkeiten an, die es gibt, um aus n verschiedenen Objekten k Objekte mit einem Griff auszuwählen.

Beispiel: Bei einem Multiple-Choice Test mit 3 Fragen (und jeweils 4 Antwortmöglichkeiten) gibt es 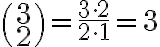 \binom {3} {2} = \frac{3 \cdot2 }{2 \cdot1 } = 3 Pfade mit genau 2 richtigen Antworten.  


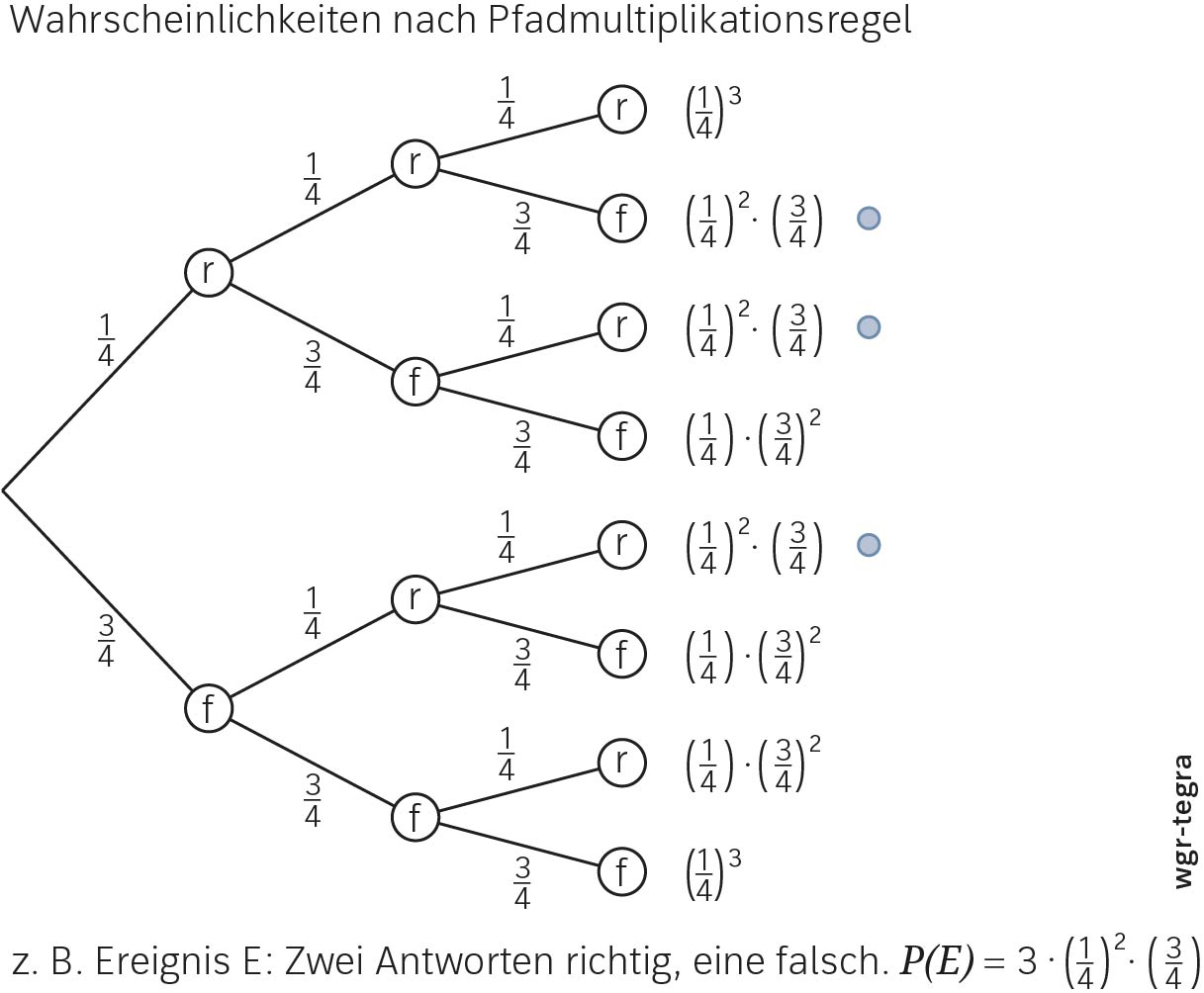
Die Zahl 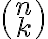 \binom {n} {k}  kann man mithilfe eines Rechners z. B. mit dem Befehl nCr(n,k) berechnen.