Infotext: Deterministische endliche Automaten (DEA)

Der Akzeptor – Ein spezieller Automat ohne Ausgabe

Bisher haben Sie sich mit der Modellierung von Problemsituationen mithilfe von endlichen Automaten beschäftigt und dabei Transduktoren kennengelernt. In der theoretischen Informatik wird oft mit einer anderen Blickweise auf endliche Automaten geschaut. Nicht die Modellierung von Ausgaben ist von Interesse, sondern das Prüfen von Befehlsfolgen (oft Eingabewörter genannt). Diese Automaten werden Akzeptoren genannt und kommen ohne Ausgaben aus. Ein Akzeptor akzeptiert ein Eingabewort genau dann, wenn sich der Automat nach Abarbeitung aller Eingabezeichen eines Eingabewortes in einem Endzustand befindet.

Ein gutes Beispiel stellt das Lampen-Szenario dar. Es lässt sich die Frage stellen, wie eine Befehlsfolge aufgebaut sein muss, die zum Anschalten aller Lichter führt. Für diese Fragestellung ist es nicht unbedingt notwendig, alle Ausgaben zu kennen. Wichtig ist hingegen, den Zustand bzw. die Zustände des Systems zu kennen, in dem alle Lichter angeschaltet sind. Ein solcher stellt einen Endzustand dar. Ist die letzte Eingabe der Befehlsfolge abgearbeitet und das System befindet sich in einem Endzustand, so lässt sich die Frage, ob alle Lichter angeschaltet, sind mit „ja“ beantworten. Der Automat akzeptiert die Befehlsfolge. Falls sich das System in einem anderen Zustand befindet, so ist die Antwort „nein“ und der Automat lehnt die Befehlsfolge ab.

Ein Akzeptor erkennt also Eingaben, die eine bestimmte Syntax besitzen. Akzeptoren werden deshalb auch erkennende Automaten genannt. Anwendungen finden solche Automaten häufig, wenn die Syntax einer Eingabe einen bestimmten Aufbau besitzen muss. Ein Beispiel aus dem Alltag wäre das Erkennen der richtigen Syntax einer E-Mail Adresse. Auch Compiler („Übersetzer“) einer Programmiersprache funktionieren nach dem Prinzip eines Akzeptors und prüfen den Quellcode auf Syntaxfehler.

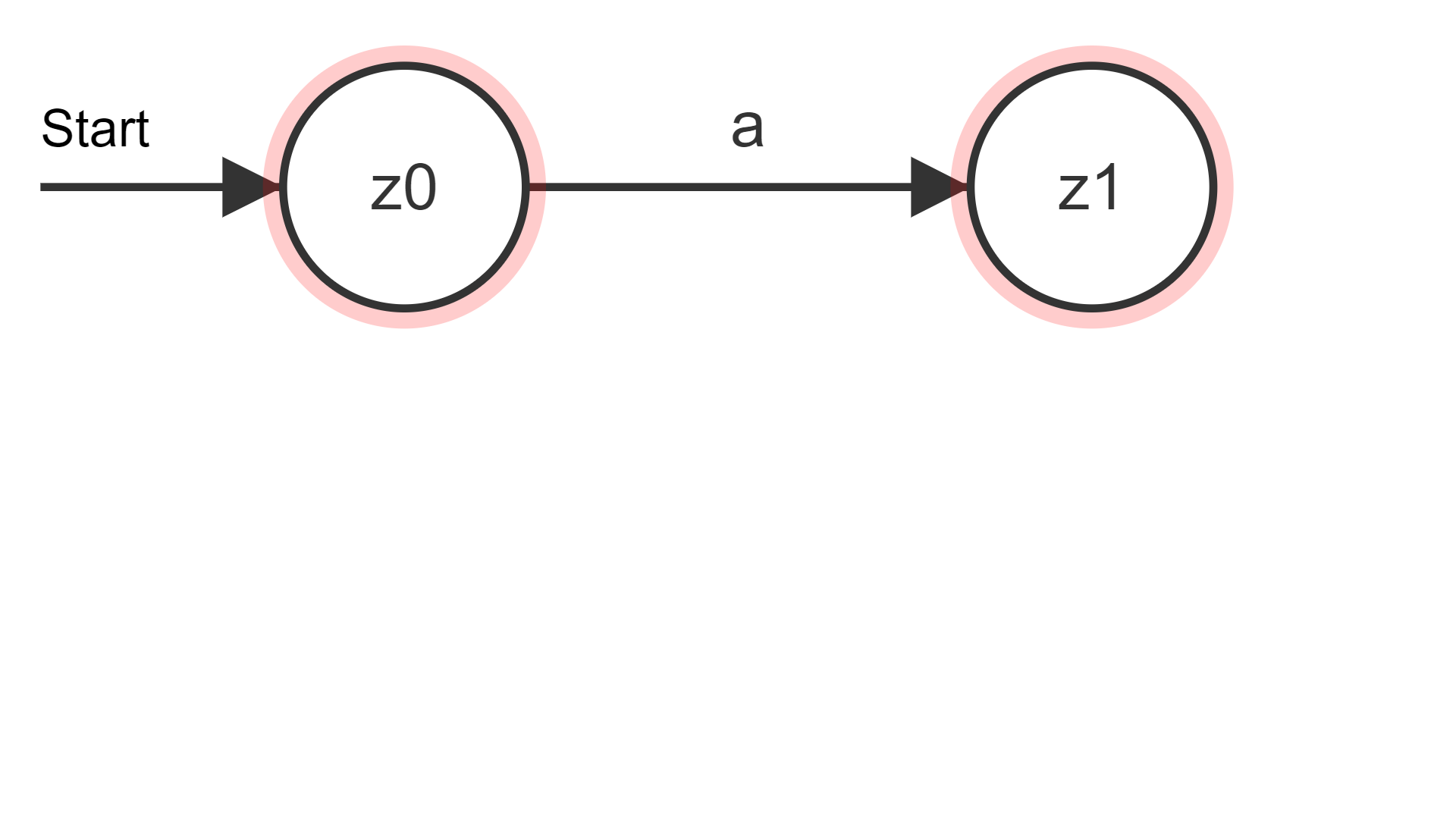
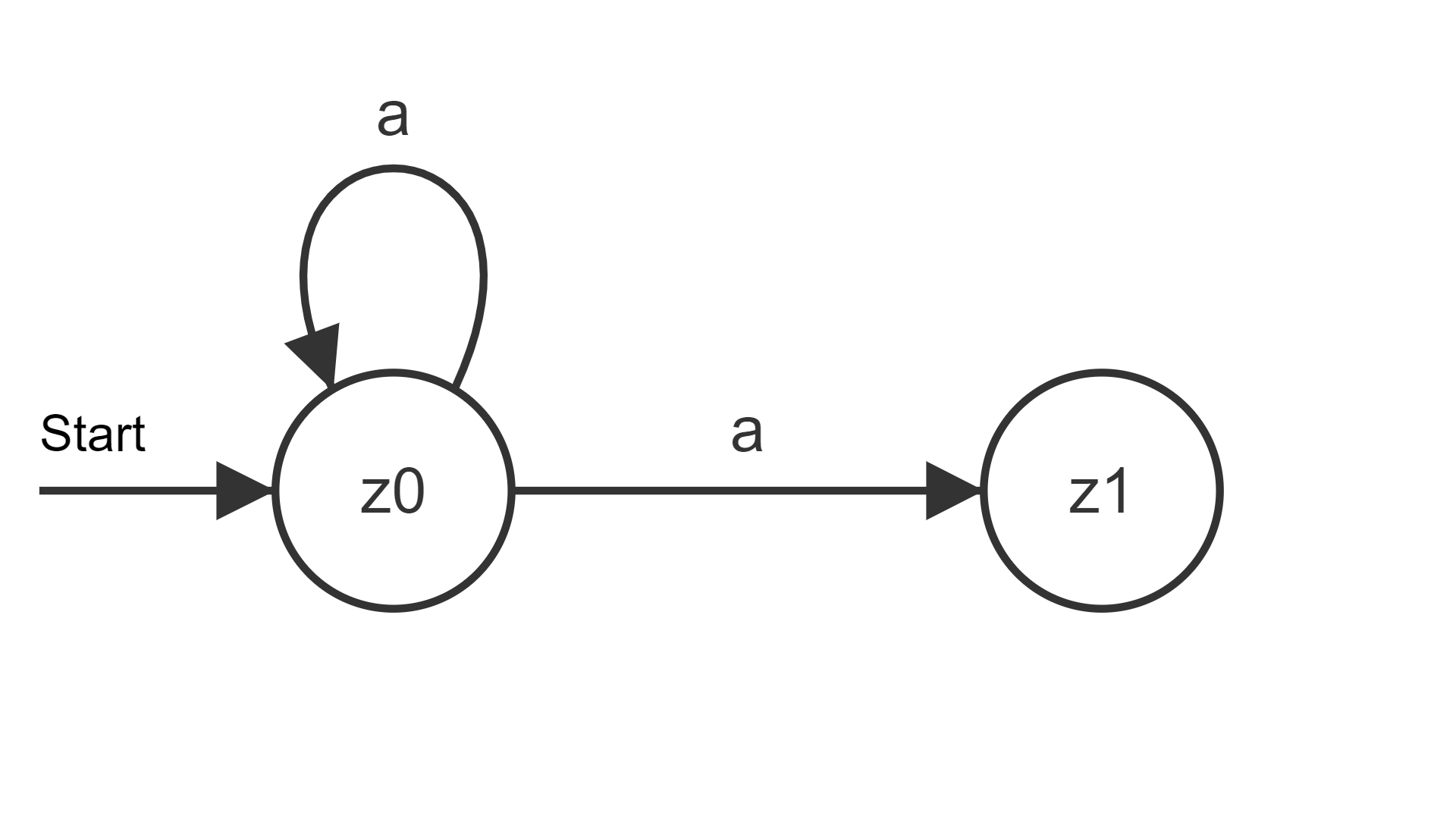
Fachkonzept: Determinismus In der theoretischen Informatik wird zum Begriff des endlichen Automaten die Bezeichnung deterministisch ergänzt. Dies sagt aus, dass in jedem Zustand eine Eingabe zu einem eindeutigen Folgezustand führt. Abbildungen 1 und 2 illustrieren diese Eigenschaft. Abb. 1: Deterministischer Übergang Abb. 2: Kein deterministischer Übergang

Definition eines Akzeptors bzw. deterministischen endlichen Automaten (DEA)

Definition: Deterministischer endlicher Automat (DEA)/Akzeptor

Ein deterministischer endlicher Automat (Akzeptor bzw. erkennender Automat) ist ein 5-Tupel A = (E, Z, δ, z₀, F), wobei gilt:

• E ist eine nicht leere, endliche Menge – das Eingabealphabet,

• Z ist eine nicht leere, endliche Menge – die Zustandsmenge,

• δ: E × Z → Z ist die Übergangsfunktion, welche jedem Eingabe-Zustands-Paar (e, z) einen Folgezustand aus Z zuordnet,

• z₀ ∈ Z ist der Anfangszustand,

• F ⊆ Z ist die Menge der Endzustände.

Wörter und Sprache eines DEA • Eine Verkettung von Eingabezeichen aus dem Eingabealphabet E wird Eingabewort w genannt. • Ein Eingabewort w wird von einem DEA genau dann akzeptiert, wenn sich nach Abarbeitung des gesamten Eingabewortes der Automat in einem Endzustand befindet. • Die Menge aller Eingabewörter, die ein DEA akzeptiert, wird in der theoretischen Informatik als Sprache L(A) eines Automaten A bezeichnet. Ein akzeptiertes Eingabewort wird dann auch Wort genannt und ist ein Teil der Sprache des Automaten.

Beispiel für einen Akzeptor und dessen Funktionsweise:

(1) Ein DEA zu ungeraden Binärzahlen

Der Automat A₁ soll als mögliche Eingabezeichen nur Nullen und Einsen besitzen – also E = {0, 1} – und Eingabewörter genau dann akzeptieren, wenn diese eine ungerade Binärzahl darstellen. Diese müssen dazu mit einer 1 beginnen und mit einer 1 enden.

Der Übergangsgraph zu A₁ sieht wie folgt aus:

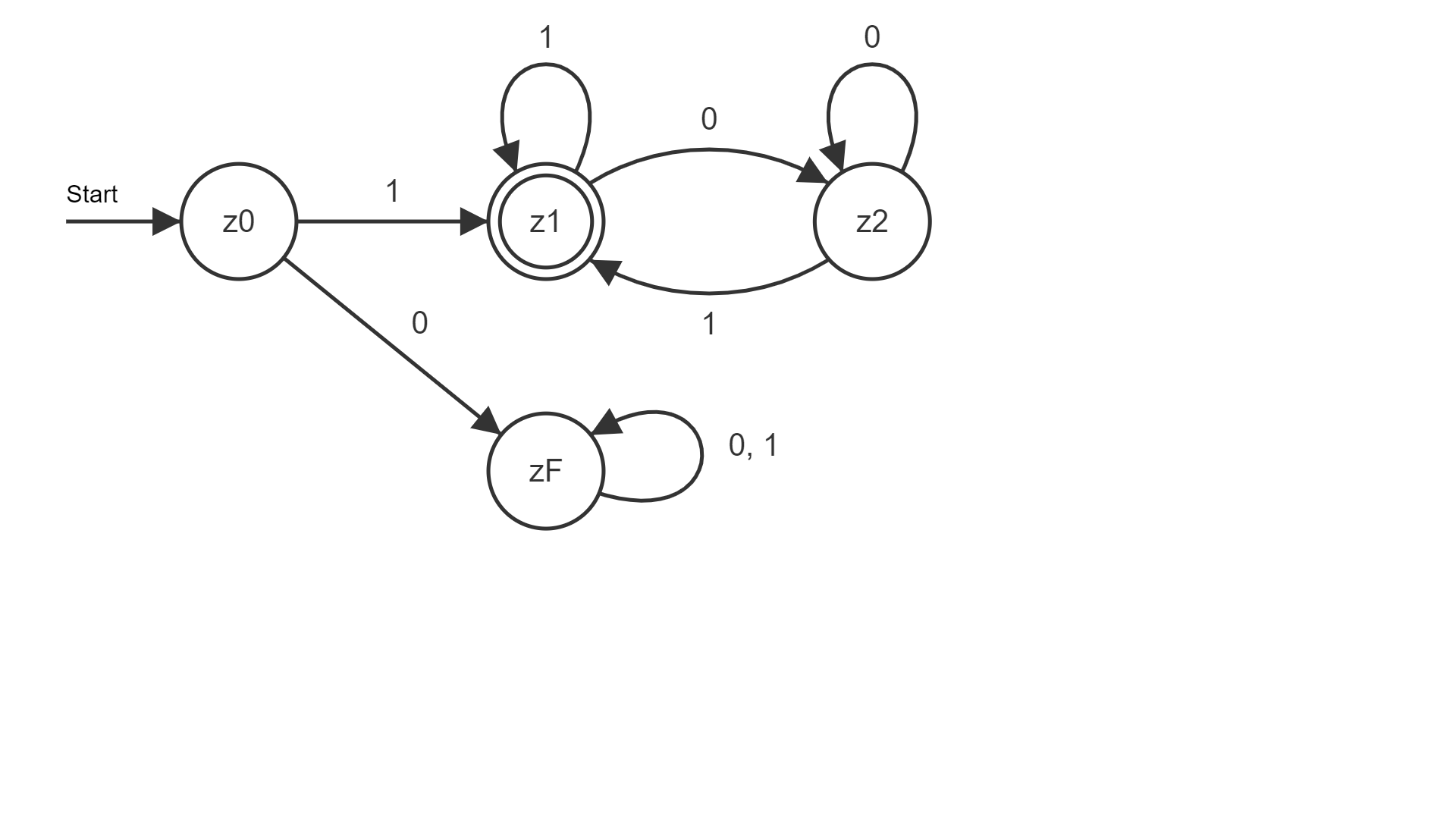
Aus dem Übergangsgraphen lassen sich folgende weitere Eigenschaften der formalen Definition von A₁ als 5-Tupel A = (E, Z, δ, z₀, F) ableiten:

• Die Zustandsmenge Z lautet: Z = {z0, z1, z2, zF},

• der Startzustand z₀ ist z0,

• die Endzustandsmenge F besteht aus nur einem Element – dem Zustand z1: F = {z1}.

(2) Prüfen eines Eingabewortes

Eingabewort:  w0 = 100101

Diagramm zu δ(w₀):

Hinweis: z1 ist in der Menge der Endzustände F. Wenn nicht, schreibe:∉ F.

w0 = 100101 wird von A₁ akzeptiert, da sich der Automat nach Abarbeitung des Eingabewortes in einem Endzustand (z1) befindet. Das Eingabewort w₀ gehört somit zur Sprache des Automaten A₁ und stellt damit ein Wort der Sprache dar. Man schreibt in diesem Fall dann: w₀ ∈ L(A₁).