Infotext: Endliche Automaten und Transduktoren
Von der zustandsbasierten Modellierung zum allgemeinen Automatenmodell
Mit den drei Lampen-Szenarien haben Sie informatische Problemsituationen kennengelernt, die man unterschiedlich modellieren konnte. Im zweiten und dritten Szenario konnten Sie erkennen, dass die Ausgabe nicht mehr nur von der Eingabe abhängt, sondern auch vom inneren Zustand des Informatiksystems. Deshalb musste dort die zustandsbasierte Modellierung mithilfe eines Übergangsgraphen gewählt werden.
Abbildung 1 veranschaulicht die gewählte Modellierung zum zweiten Szenario an einem Beispiel. Dort wurde als erste Eingabe der rote Knopf gedrückt („r“). Da der Anfangszustand z0 ist wird von diesem aus der Folgezustand generiert. Dieser stellt bei Eingabe
von „r“ den Zustand z1 dar. Aus der letzten Unterrichtseinheit wissen wir, dass bei Erreichen des Zustands z1 nur die zweite Lampe leuchtet. Somit erfolgt die Ausgabe „100“.
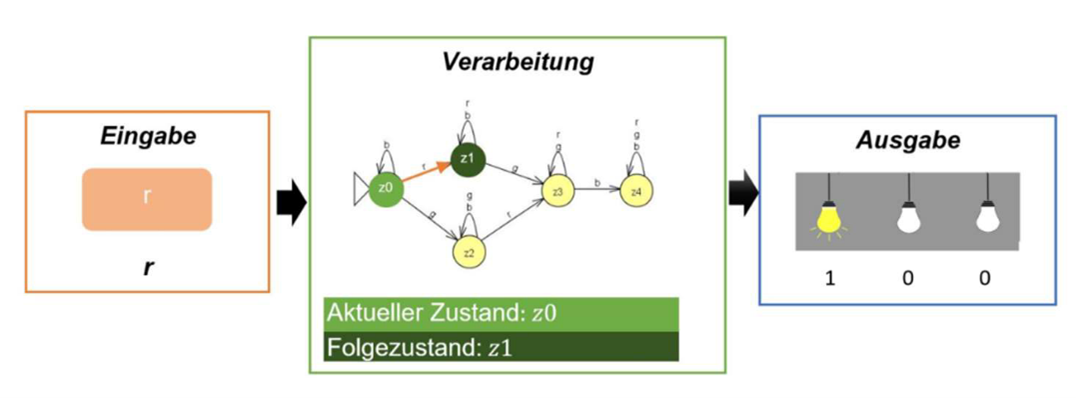
Abb. 1: Verhaltensweise des Informatiksystems zum zweiten Szenario bei Drücken des roten Buttons zu Beginn.
Informatiksysteme, die Eingaben schrittweise verarbeiten und dessen innere Funktionsweise auf der zustandsbasierten Modellierung beruhen, nennt man auch endliche Automaten. Aus der Abbildung 1 und des Settings eines Lampen-Szenarios
lassen sich folgende Bestandteile eines endlichen Automaten abstrahieren:
|
Definition: Allgemeines Modell eines endlichen Automaten Ein endlicher Automat, der ein interaktives Informatiksystem modelliert besitzt unabhängig von seiner konkreten Umsetzung folgende Eigenschaften:
|
|---|
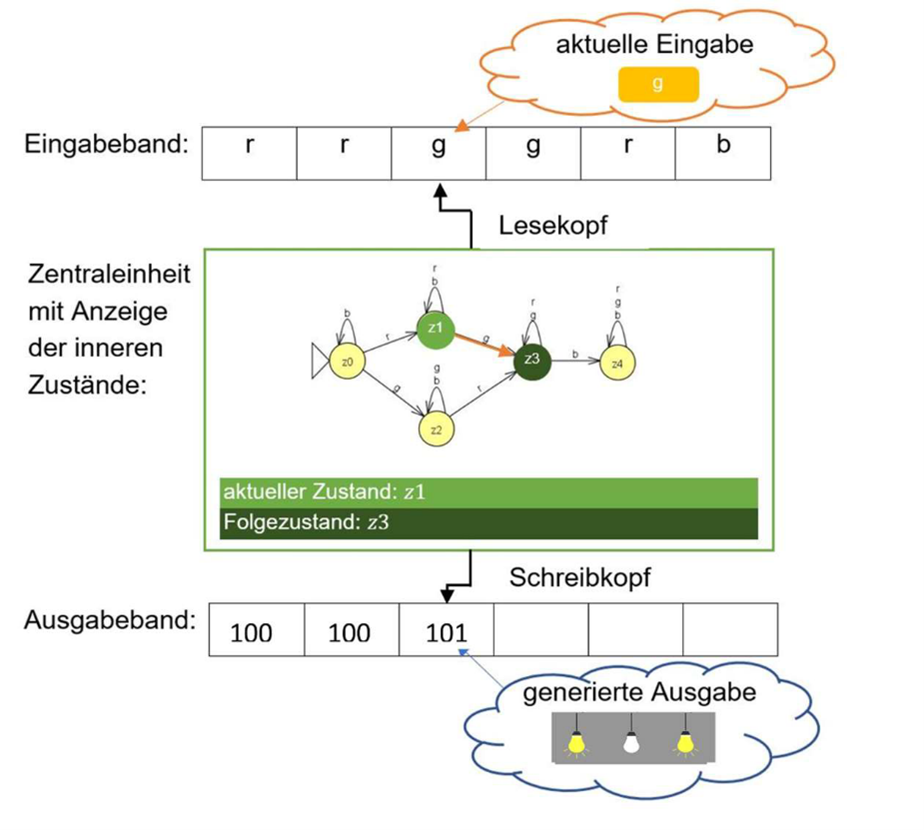
Visualisierung am Beispiel des zweiten Lampen Szenarios:
Transduktoren – Endliche Automaten mit Ausgabe
Ein Beispiel für endliche Automaten sind sogenannte Transduktoren. Bei diesen werden für jede Eingabe nicht nur ein Folgezustand definiert, sondern auch eine Ausgabe generiert. Aus diesem Grund werden Transduktoren auch endliche Automaten mit Ausgabe genannt. Um diese vollständig zu beschreiben benötigt es ein Eingabealphabet, das alle Eingaben enthält, die möglich sind und auf das Eingabeband geschrieben werden dürfen. Darüber hinaus muss auch das Ausgabealphabet festgelegt werden. Für die Beschreibung des inneren Verhaltens des Systems können Übergangsgraphen oder Übergangstabellen angefertigt werden. Aus diesem lassen sich die Zustandsmenge und die Übergangsfunktion ableiten. Darüber hinaus wird ein Startzustand festgelegt, der im Übergangsgraphen gekennzeichnet wird.
Abb. 2: Eine einfache Schaltung als Mealy-Automat:
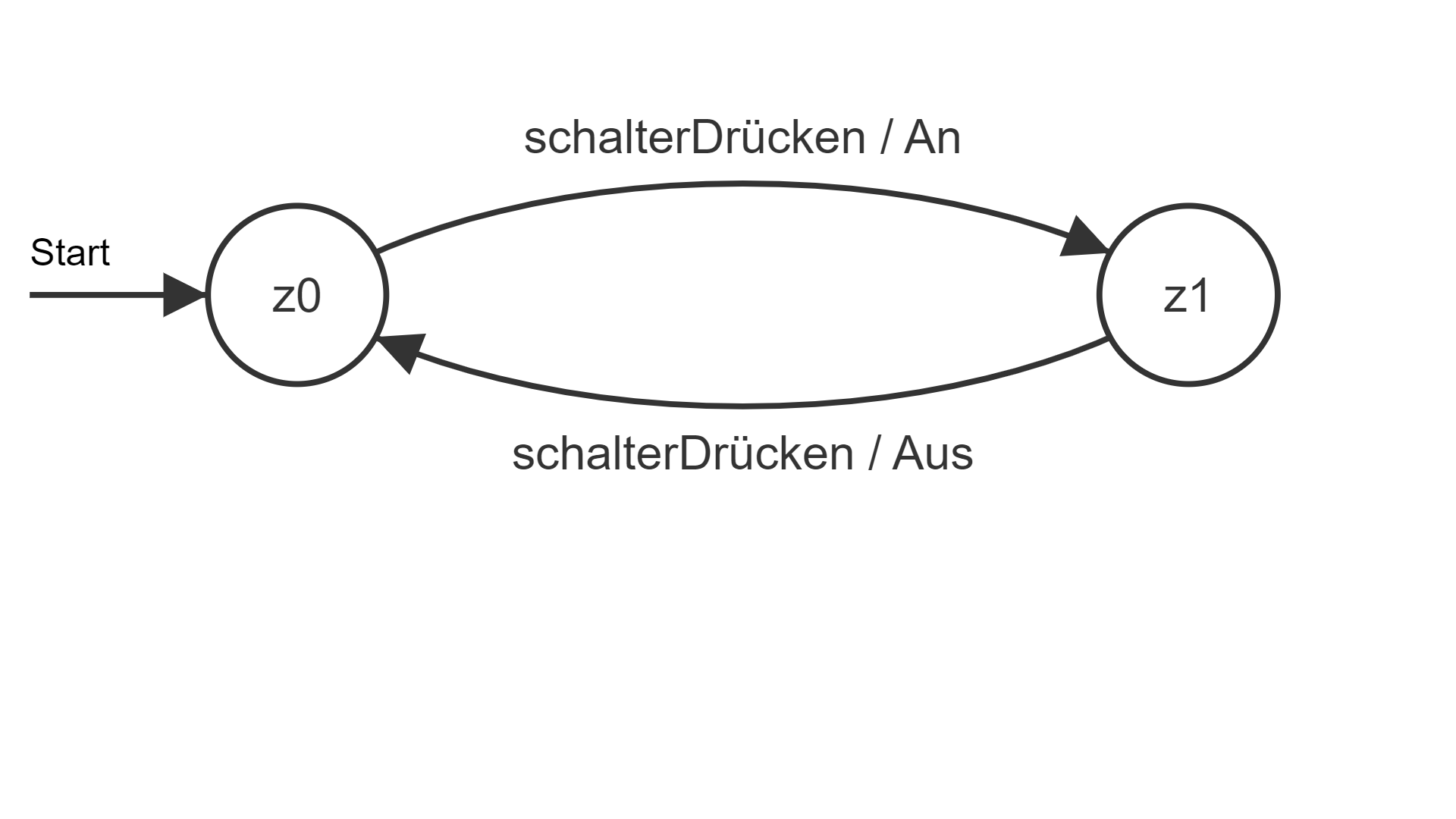
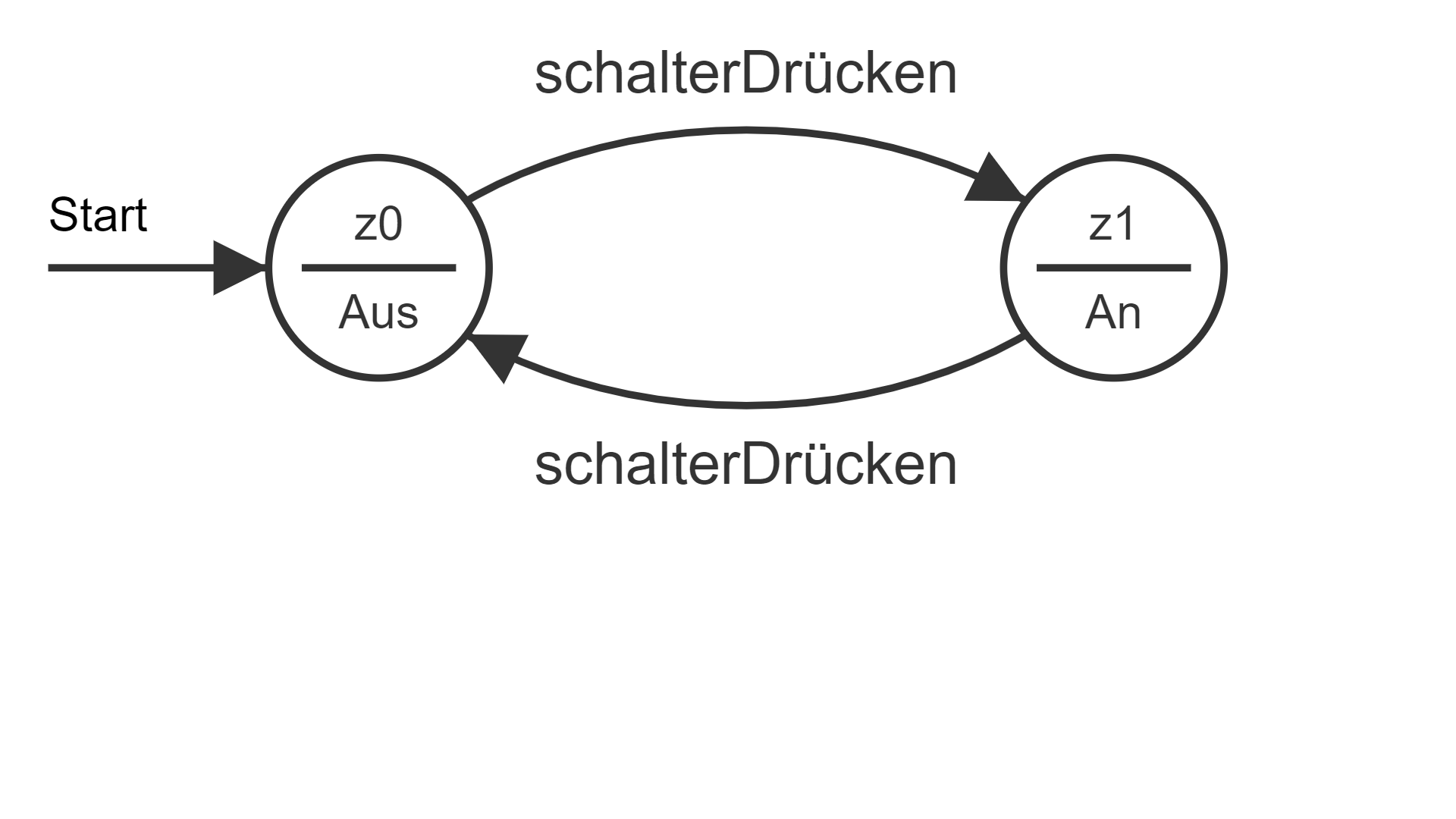
Abb. 3: Eine einfache Schaltung als Moore-Automat:
Definition: Transduktoren - Mealy-Automat & Moore-Automat
|
Ein Mealy-Automat M = (E, A, Z, δ, λ, z0) ist ein deterministischer, endlicher Automat mit Ausgabe. Es gilt:
Ein Moore-Automat M = (E, A, Z, δ, λ, z0) lässt sich analog definieren. Einziger Unterschied ist die Definition der Ausgabefunktion λ. Diese ordnet jedem Zustand z ein eindeutiges Ausgabezeichen a aus dem Ausgabealphabet A zu (kurz: λ: Z → A). Die Übergangsfunktion und die Ausgabefunktion können zusammen als Übergangsgraph (siehe Abb. 2 u. Abb. 3) oder Übergangstabelle angegeben werden. Auch eine separate Angabe in Form einer Tabelle ist möglich. |
|---|
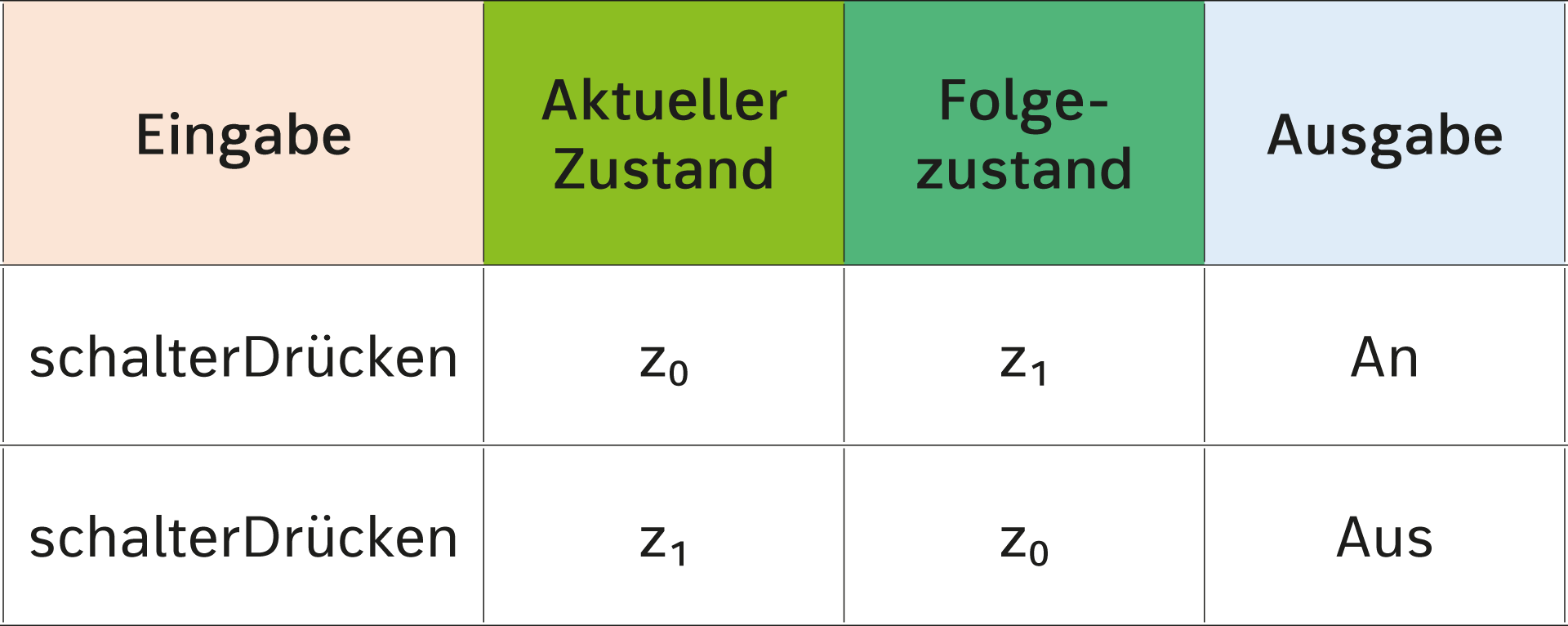
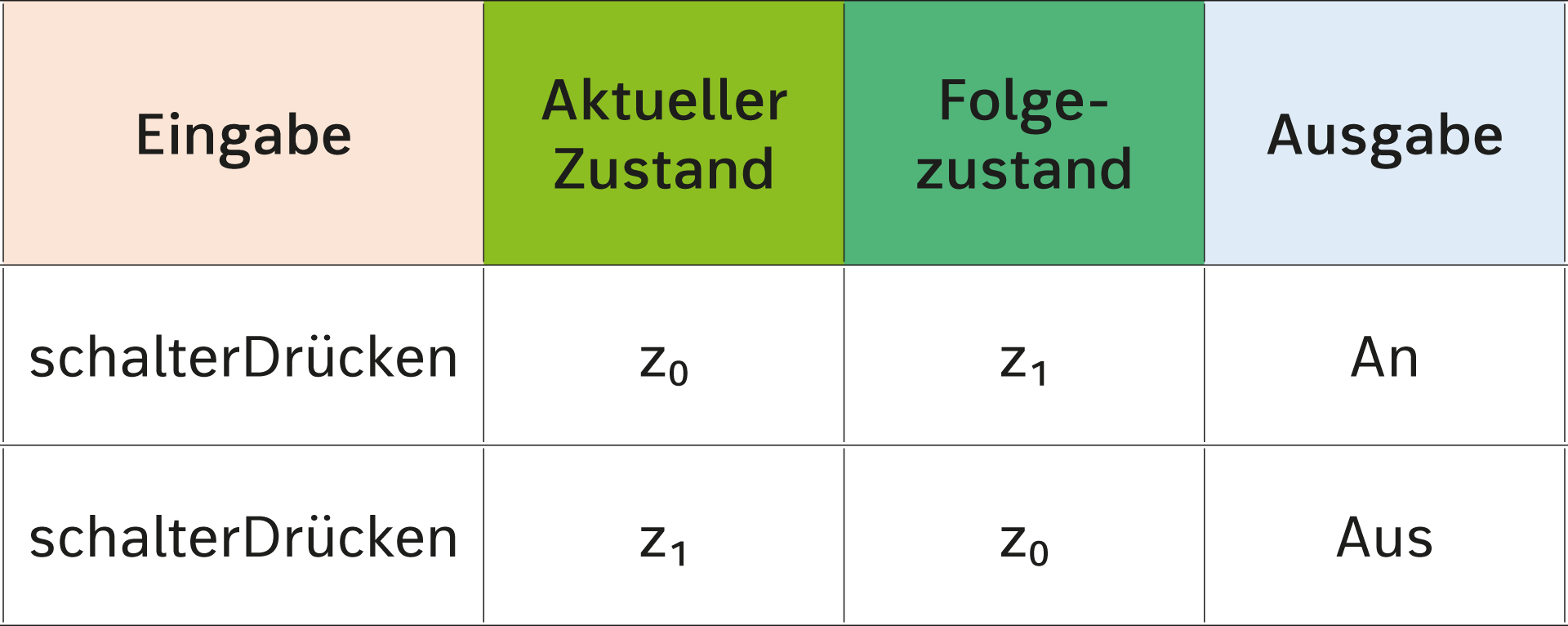
Eine einfache Schaltung, wie in Abb. 2 u. 3 dargestellt, lässt sich als Mealy-Automat und als Moore-Automat darstellen:
|
Mealy-Automat Der Mealy-Automat zur Schaltung ist definiert als 5-Tupel M1 = (E, A, Z, δ, λ, z0). E = {schalterDrücken} Mögliche Visualisierungen der Ausgabefunktion λ und der Übergangsfunktion δ: Übergangsgraph:
Übergangstabelle:
Tabellen zur Ausgabe- und Zustandsübergangsfunktion: Zustandsübergangstabelle zur Übergangsfunktion δ:
Ausgabetabelle zur Ausgabefunktion λ:
|
Moore-Automat Der Moore-Automat zur Schaltung ist definiert als 5-Tupel M2 = (E, A, Z, δ, λ, z0). E = {schalterDrücken} Mögliche Visualisierungen der Ausgabefunktion λ und der Übergangsfunktion δ: Übergangsgraph:
Übergangstabelle:
Tabellen zur Ausgabe- und Zustandsübergangsfunktion: Zustandsübergangstabelle zur Übergangsfunktion δ:
Ausgabetabelle zur Ausgabefunktion λ:
|