3 Zählstrategien
Leon hat bei einem Test mit 5 Fragen seine Antworten
zufällig angekreuzt. Er hat erfahren, dass er bei genau drei Fragen die richtige Antwort angekreuzt hat. Er weiß nur nicht welche. Er überlegt wie viele Möglichkeiten
es dafür gibt:
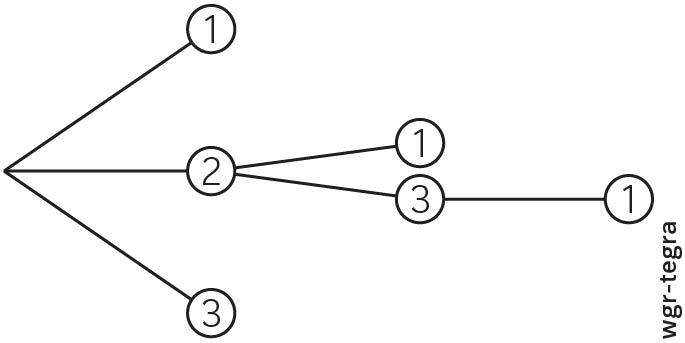
„Ich wähle dazu aus den Zahlen von 1 bis 5 einfach 3 aus. Für die erste Zahl
gibt es 5 Möglichkeiten, für die zweite Zahl nur noch 4, für die dritte Zahl
nur noch 3. Also gibt es dafür insgesamt 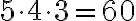 Möglichkeiten.“
Möglichkeiten.“
Seine Freundin Clara sagt: „Das stimmt nicht ganz, die Reihenfolge
der Zahlen spielt hierbei keine Rolle. Es ist nämlich egal ob du z. B. 3,1,2
oder 1,2,3 betrachtest. Du musst also dein Ergebnis noch durch die Anzahl der
Möglichkeiten dividieren, die es für die Anordnung von 3 verschiedenen Zahlen
gibt.“
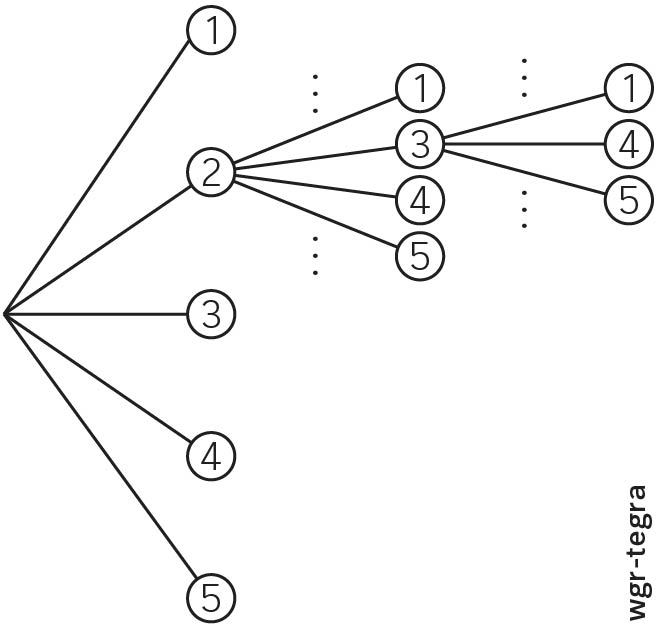
Leon überlegt: „Ich schreibe eine dreistellige Zahl aus drei verschiedenen
Ziffern. Für die erste Ziffer gibt es 3 Möglichkeiten, für die zweite Ziffer
nur noch 2 und für die dritte Ziffer nur noch eine. Das sind also insgesamt 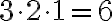 Möglichkeiten. Also
gibt es insgesamt
Möglichkeiten. Also
gibt es insgesamt 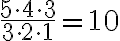 Möglichkeiten, aus den 5 Fragen zufällig drei
richtig zu beantworten.“
Möglichkeiten, aus den 5 Fragen zufällig drei
richtig zu beantworten.“