Glossar
Hier könnt ihr alle Fachbegriffe sammeln und mit einer Erklärung speichern.
@ | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | Alle
F |
|---|
FunktionFunktionen sind
eindeutige Zuordnungen. Das sind Zuordnungen, bei denen es zu jedem x-Wert
genau einen y-Wert gibt. Dieser eindeutig bestimmte y-Wert wird auch Funktionswert
an der Stelle x genannt | |
Funktionswert | |
N |
|---|
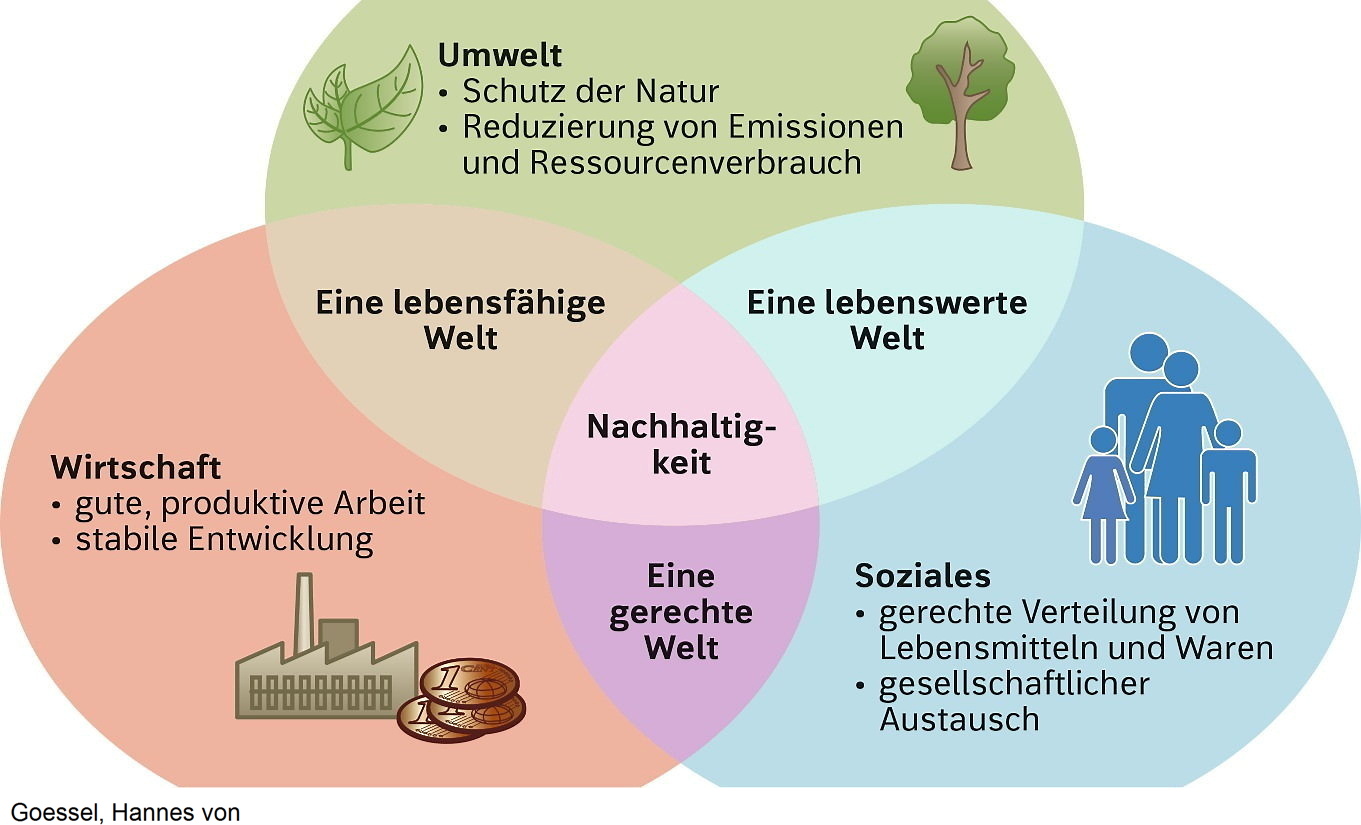
Nachhaltigkeit
| |
P |
|---|
PunktprobeMit einer Punktprobe wird rechnerisch überprüft, ob ein gegebener Punkt P (x0|y0) auf dem Graphen einer Funktion f liegt. Wenn f(x0) = y0 gilt, dann liegt P auf dem Graphen von f. (Beispiel: Gegeben ist der Punkt P(2|7) und die Funktion f mit der Funktionsgleichung f(x) = 2,5 · x + 3; da f(2) = 2,5 · 2 + 3 = 8 ≠ 7 gilt, liegt P nicht auf dem Graphen von f.) | |
S |
|---|
SteigungDie Steigung m einer linearen Funktion f mit der Funktionsgleichung f(x) = m · x + b gibt an, um wie viel sich der Funktionswert f(x) ändert, wenn x um 1 vergrößert wird. | |