8 Aufgaben zur Selbstkontrolle
| Website: | LOGINEO NRW LMS |
| Kurs: | [Demo] M-Q1/Q2-12/13-GY: Modellieren mit Binomialverteilung |
| Buch: | 8 Aufgaben zur Selbstkontrolle |
| Gedruckt von: | Gast |
| Datum: | Freitag, 6. März 2026, 22:59 |
1. Studierende und Laptops
Befragungen haben ergeben, dass 80% der Studierenden über einen Laptop verfügen.
- Berechnen Sie die Wahrscheinlichkeit, dass von 12 Personen genau die Hälfte einen Laptop hat.
- Berechnen Sie die Wahrscheinlichkeit, dass von 15 Personen genau zwölf einen Laptop haben.
1.1. Lösung: Studierende und Laptops
Lösung zu a
Zufallsgröße X: Anzahl der Personen mit Laptop
Wahrscheinlichkeit für einen Treffer: p = 0,8
Wahrscheinlichkeit für einen Treffer: 1 - p = 0,2
Länge der Bernouli-Kette: n = 12
Anzahl der Pfade: ![]()
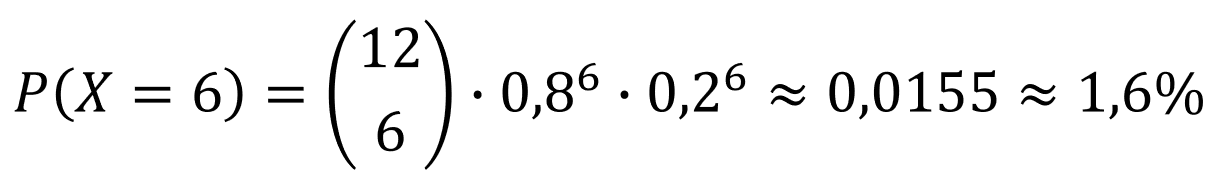
Lösung zu b
Zufallsgröße X: Anzahl der Personen mit Laptop
Wahrscheinlichkeit für einen Treffer: p = 0,8
Wahrscheinlichkeit für einen Fehlschlag: 1 - p = 0,2
Länge der Bernouli-Kette: n = 15
2. Glücksrad
Ist das viermalige Drehen des Glücksrades eine Bernoulli-Kette?
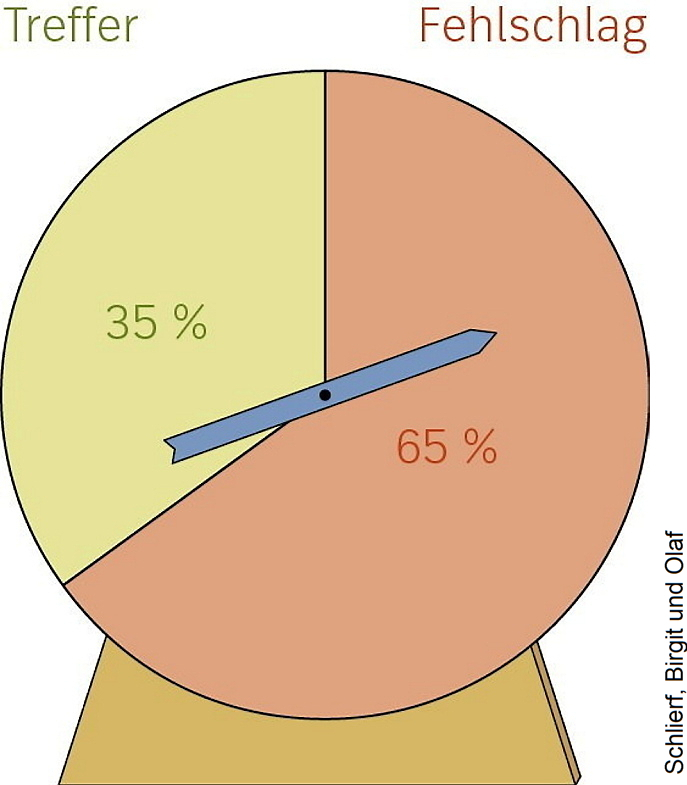
2.1. Lösung: Glücksrad
3. Binomialverteilung richtig angewendet?
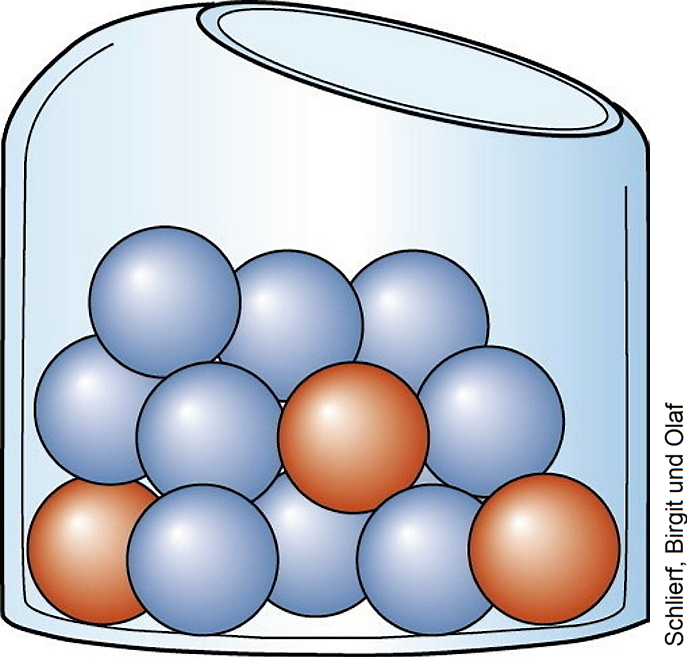
Aus einer Urne mit drei roten und neun blauen Kugeln werden fünf Kugeln nacheinander ohne Zurücklegen gezogen. Wie groß ist die Wahrscheinlichkeit, dass dabei genau drei rote Kugeln gezogen werden?
Peter rechnet: 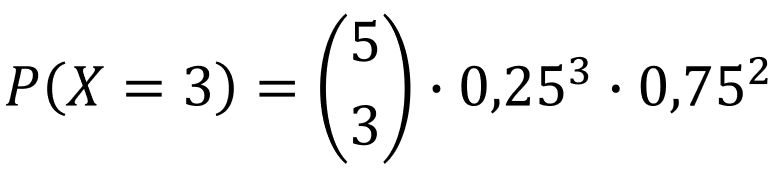
Warum "passt" diese Formel nicht?
3.1. Lösung: Binomialverteilung richtig angewendet?
Man darf die Binomialverteilung nicht anwenden, da sich bei den fünf Ziehungen ohne Zurücklegen die Trefferwahrscheinlichkeit P (rot) bei jeder Ziehung ändert.
4. Baumdiagramme
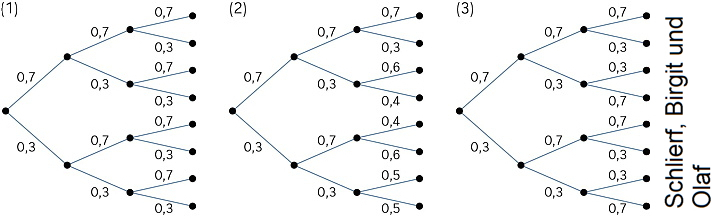
Welches der Baumdiagramme passt zu einer Bernouli-Kette? Begründen Sie!
4.1. Lösung: Baumdiagramme
(1) Bernoulli-Kette: ja
- n = 3
- P („Treffer“) = 0,7
- Trefferwahrscheinlichkeit ist auf allen drei Stufen gleich.
(2) Bernoulli-Kette: nein
- n = 3
- Trefferwahrscheinlichkeiten hängen davon ab, welches Ergebnis auf der vorigen 3 Stufe eingetreten ist.
(3) Bernoulli-Kette: nein
- n = 3
- Trefferwahrscheinlichkeiten hängen davon ab, welches Ergebnis auf der vorigen Stufe eingetreten ist:
Auf der ersten Stufe ist P ("Treffer“) = 0,7. Einem Treffer auf der ersten Stufe folgt ein Treffer auf der zweiten Stufe mit einer Wahrscheinlichkeit von 0,3. Das Ergebnis auf der ersten Stufe beeinflusst also die Wahrscheinlichkeit eines Treffers auf der zweiten Stufe.