4 Basiswissen Binomialverteilung
| Website: | LOGINEO NRW LMS |
| Kurs: | [Demo] M-Q1/Q2-12/13-GY: Modellieren mit Binomialverteilung |
| Buch: | 4 Basiswissen Binomialverteilung |
| Gedruckt von: | Gast |
| Datum: | Montag, 15. Dezember 2025, 12:54 |
1. Bernoulli-Formel
Bernoulli-Formel
Bei einer n-stufigen Bernoulli-Kette mit der Erfolgswahrscheinlichkeit p betrachtet man die Anzahl X der Erfolge. Die Wahrscheinlichkeit für genau k Erfolge wird mitP(X =k) bezeichnet und wie folgt berechnet:
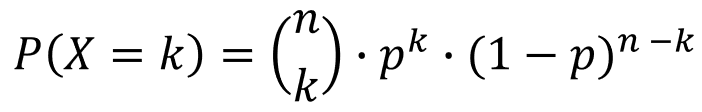
Dabei gibt der Binomialkoeffizient
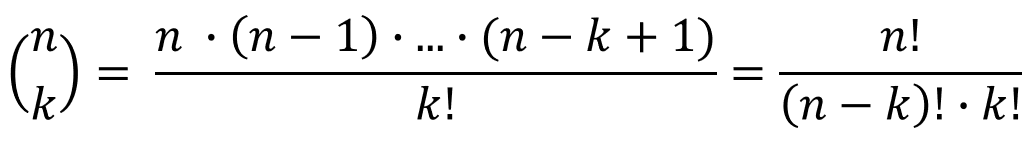
die Anzahl der Pfade mit genau k Erfolgen im
n-stufigen Baumdiagramm der Bernoulli-Kette an.
ist die
Wahrscheinlichkeit für k Erfolge und n-k Misserfolge am Ende eines Pfades im
Baumdiagramm.
Berechnung von P(X =k) mithilfe eines Rechnerbefehls: binomPdf(n, p, k)
Erklärvideo zur Bernoulli-Formel:
Steckbrief für ein Beispiel
- Bernoulli-Kette der Länge 4
- Trefferwahrscheinlichkeit 0,4
- Wahrscheinlichkeit für einen Fehlschlag:
1 -0,4 = 0,6
Berechnung der Wahrscheinlichkeit für genau 2 Treffer:
- Anzahl der Pfade der Lange 4 mit genau 2 Treffern:
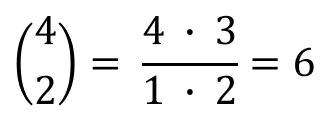
- Wahrscheinlichkeit für jeden Pfad mit genau 2 Treffern:
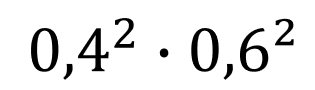
- Wahrscheinlichkeit für genau 2 Treffer:
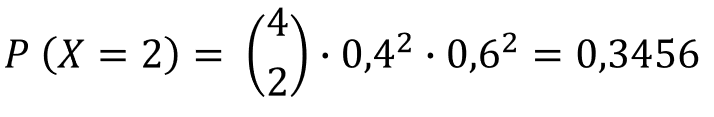
2. Binomialverteilung
Bei
einer Bernoulli-Kette wird in der Regel die Anzahl X der Erfolge betrachtet.
Die Wahrscheinlichkeitsverteilung der Anzahl X der Erfolge nennt man Binomialverteilung.
tabellarisch
| Anzahl der Erfolge k |  | |
|---|---|---|
| 0 |  | 0,1296 |
| 1 |  | 0,3456 |
| 2 |  | 0,3456 |
| 3 |  | 0,1536 |
| 4 |  | 0,0256 |
grafisch
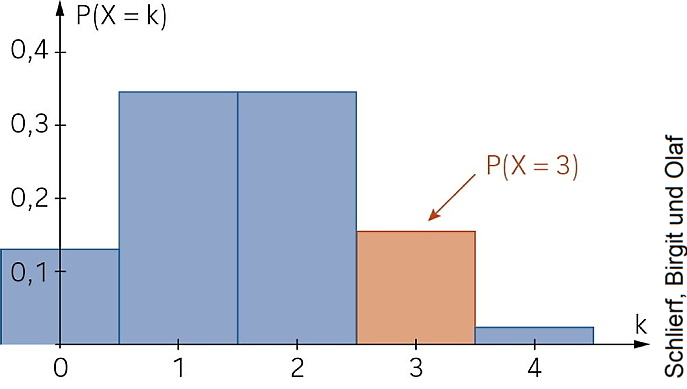
Die grafische Darstellung heißt Histogramm.